Part A
A person holds a 10 kg box against a smooth (i.e. frictionless) wall (as it slides down) by applying a perfectly horizontal force of 300 N. What is the magnitude of the normal force exerted on the box by the wall?
Solution
System:
Box as point particle.
Interactions:
External influences from the earth (gravity), the wall (normal force) and the person (applied force).
Model:
Approach:
Diagrammatic Representation
We begin with a free body diagram for the box:
It is important to note that any surface has the potential to exert a normal force and that the normal is always perpendicular to the plane of the surface. If the wall did not exert a normal force, the box would simply pass through it.
Mathematical Representation
From the free body diagram, we can write the equations of Newton's 2nd Law.

Because the box is held against the wall, it has no movement (and no acceleration) in the x direction (ax = 0). Setting ax = 0 in the x direction equation gives:

Part B
A person moves a 10 kg box up a smooth wall by applying a force of 300 N. The force is applied at an angle of 60° above the horizontal. What is the magnitude of the normal force exerted on the box by the wall?
Solution
System:
Box as point particle.
Interactions:
External influences from the earth (gravity), the wall (normal force) and the person (applied force).
Model:
Approach:
Diagrammatic Representation
We begin with a free body diagram for the box:
Mathematical Representation
From the free body diagram, we can write the equations of Newton's 2nd Law.
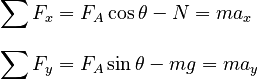
Because Because the box is held against the wall, it has no movement (and no acceleration) in the x direction (ax = 0). Setting ax = 0 in the x direction equation gives:
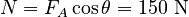
Part C
A person scrapes a 10 kg box along a low, smooth ceiling by applying a force of 300 N at an angle of 30° above the horizontal. What is the magnitude of the normal force exerted on the box by the ceiling?
Solution
System:
Box as point particle.
Interactions:
External influences from the earth (gravity), the ceiling (normal force) and the person (applied force).
Model:
Approach:
Diagrammatic Representation
We begin with a free body diagram for the box:
The ceiling must push down to prevent objects from moving up through it.
Mathematical Representation
From the free body diagram, we can write the equations of Newton's 2nd Law.
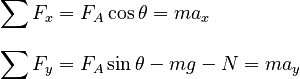
Because Because the box is held against the ceiling, it has no movement (and no acceleration) in the y direction (ay = 0). Setting ay = 0 in the y direction equation gives:

which we solve to find:
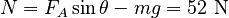
We can check that the y direction is in balance. We have N (52 N) and mg (98 N) on one side, and FA,y on the other (150 N).





