The gravitational force exerted by the earth on an object near the earth's surface.

The Force of Gravity Near Earth's Surface

Defining "Near"

Suppose an object of mass m is at a height h above the surface of the earth. Assume that the earth is spherical with radius RE. Working in spherical coordinates with the origin at the center of the earth, the gravitational force on the object from the earth will be:


A Taylor expansion gives:


Thus, for h/RE << 1, the gravitational force from the earth on the object will be essentially independent on altitude above the earth's surface and will have a magnitude equal to:

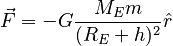
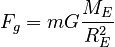
Defining g

The above expression is of the form:


if we take:

Gravitational Potential Energy Near Earth's Surface

Near the earth's surface, if we assume coordinates with the +y direction pointing upward, the force of gravity can be written:

Since the "natural" ground level varies depending upon the specific situation, it is customary to specify the coordinate system such that:

The gravitational potential energy at any other height y can then be found by choosing a path for the work integral that is perfectly vertical, such that:

For an object in vertical freefall (no horizontal motion) the associated potential energy curve would then be:

For movement under pure near-earth gravity, then, there is no equilibrium point. At least one other force, such as a normal force, tension, etc., must be present to produce equilibrium.

Example Problems involving Near-earth Gravity

Example Problems involving Gravitational Force

Content by label

There is no content with the specified labels

Example Problems involving Gravitational Potential Energy