Definitions of Position and Velocity
If we start knowing the position vs. time x ( t ), then the velocity, v ( t ), is the derivative of its position, and the derivative in turn of this velocity is the particle's acceleration, a ( t ). The force is the particle's mass times a ( t ).
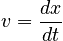
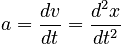
In fact, as you can see, the velocity and acceleration are defined as derivatives of the position, a fact acknowledged by the phrase "the calculus of motion". Newton had to invent calculus of one variable to deal with motion!
