Overview
Distinguishable and indistinguishable particles have been considered. Consider the single-particle partition function among distinguishable particles. Label and assign criteria among different particles. Apply the Boltzman approximation at high temperature, low density, and high mass to indistinguishable particles and obtain the relation below. Adjust for overcounting. The number of particles is much less than the number of state. Apply to a monoatomic gas. At low temperature and high density, the Boltzman approximation is not good. Different types of statistics have been mentioned.
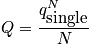
Today a diatomic gas is considered. In a solid, atoms are fixed in space. A solid solution and vibrations in a solid are considered.
Degrees of freedom in a diatomic molecule
There are different degrees of freedom in a diatomic molecule. Below is a schematic.
There are various contributions to the Hamiltonian of a single particle. Contributions include translation, rotation, vibration, electric, and nuclear. The diatomic molecule is part of an ideal gas. Separate the Hamiltonians. Separate the interactions and particles. Under the rigid rotor approximation, rotations do not see the changing bond length. The contributions of the Hamiltonian due to rotation and vibration are independent. When vibrations are large, though, the bond length is changing. The first excited electric state would be considered. McQuarrie considers the first excited nuclear state. Thermodynamics cares about derivatives of the partition function.
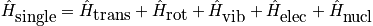
The partition function is a measure of the number of thermally excited states. Consider the single-particle partition function.
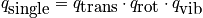
There is a high temperature approximation. Assuming "normal conditions" the Boltzman approximation can be used.
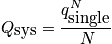
Translation
Look at the center of mass when considering the translational component of the single-particle partition function.
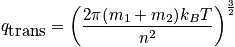
Vibrations
There is interest in expressions of
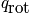
and
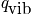
and energy spectrum. Diatomic molecules see a potential well and there is an equilibrium bond length. The deviation is
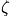
, and the term
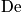
is the energy required to dissociate. Assuming the vibrations are small, the energy associated with vibrating bonds can be expressed with a Taylor expansion.
!Potential_versus_spacing_--_Ro.PNG!
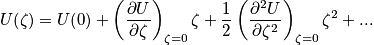
The first term,
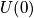
, is constant, and the second term is equal to zero since there is no force. The second-order term is proportional to the strength of the bond between two particles. There is a force constant between two particles. Write the Hamiltonian with the approximation of small vibrations.
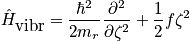
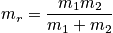
The first term is a kinetic contribution, and the force constant,f, is a property of the molecule. Consider the quantum mechanical solutions of a harmonic oscillator.
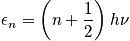
<P> </P>
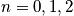
<P> </P>
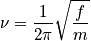
There is a relation between a spring constant and mass. Light masses or masses with a stiff spring vibrate rapidly. Write the mini-partition function. and simplify with the relation pertaining to a geometric series.
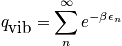
<P> </P>
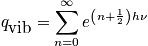
<P> </P>
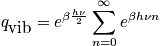
<P> </P>
<P> </P>

<P> </P>
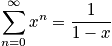
<P> </P>
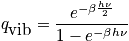
Express in terms of the characteristic vibrational temperature,
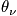
.
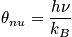
<P> </P>
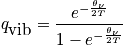
The characteristic termperature,
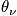
, is typically between
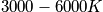
. Calculate the probability of being in a certain state.
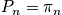
<P> </P>
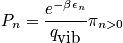
A general expression of being in any state other than the ground state is below, as well as a calculation at
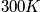
and a characteristic temperature of
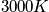
.
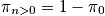
<P> </P>
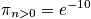
<P> </P>
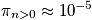
The probability of a molecule being in an excited state is very small. It is hard to excite a vibrational state above the ground state.
Rotation
Rotational motion is associated with angular momentum. The rotation of a diatomic molecule can be considered equivalent to the rotation of one particles moving freely along a sphere with fixed radius,
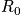
, and a reduced mass. Consider the Hamiltonian. The term
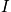
is the moment of inertia and an expression of the eigenvalues,
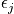
, to the spherical coordinate problem is below.
!Diatomic_molecule_--_rotation_with_axis.PNG!
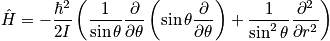
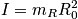
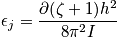
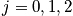
Identify the Hamiltonian, solve with Schrodinger or remember the energy spectrum. In an unsymmetric molecules, the two masses are not equivalent. A summation in the mini-partition function is not as easy as the vibrational case. Consider two limits.
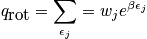
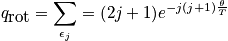
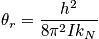
Case 1
The first case involves high temperatures, or temperatures much greater than\theta_r. If the temperature is large, the exponential term goes to zero. States are dense, and it is possible to approximate with an integral.
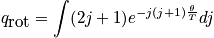
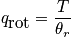
Case 2
Consider when the temperature is close to\theta_r. Caclulate a few of the terms, and see that the terms decrease rapidly. Assume that the larger terms are zero. Consider the first couple terms of the summation.
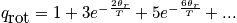
There is overcounting of the number of states with symmetric molecules. Rotational degrees of freedom are coupled. Read MacQuarrie 6-4. The level of quantum mechanics is above what is required. There is inversion of the nucleus, two indistinguishable configurations, and overcounting. Regarding the quiz, one should be able to do a problem with a symmetric molecule.
Correction for overcounting
The mini-partition function is a measure of the number of thermally accessible states. The mini-partition function of rotation is written below in the first case wherein the temperature is much greater than\theta_r.
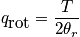
The case where the temperature is less than\theta_rrequires rigorous quantum mechanical treatment (really onlyH_2!). Calculate the probability to be in a certain state.
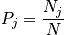
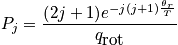
Other states are seen other than the lowest one. A graph is below.
!Nj_n_versus_j.PNG!
Deriving Thermodynamic Quantities from Partition Function
From the single-partition function, build the entire system.
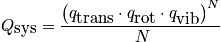
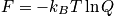
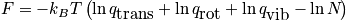
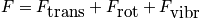
Pressure
Calculate the pressure. Only the translational component of the partition function is proportional to volume.

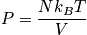
This expression is the same as for a monoatomic gas. The ideal gas equation holds for both monoatomic and diatomic gases.
Heat Capacity
Calculate the heat capacity. Decouple energies and heat capacities.
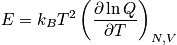
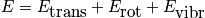
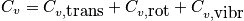
Translational energy
Below is an expression of the translational energy

Rotational energy
An expression of the rotational energy is below. Consider at normal temperature and a system that is notH_2. An expression of the rotational partition function is also below.
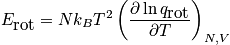
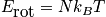
Vibrational energy
The vibrational energy is expressed below.
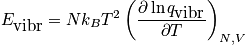
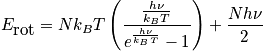
Analyze the vibrational energy with two limits.
Case 1
In the first case, consider the vibrational energy as the temperature approaches infinity. The expression of vibrational energy can be written in terms ofx, and is written below. As the temperature approaches infinity,xapproaches zero.
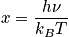
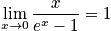
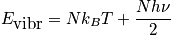
Case 2
An expression of the vibrational energy in the case of temperature much less than
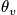
.
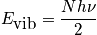
Translational component of heat capacity
The translational component of heat capacity is found by differentiating the translational energy with respect to temperature.
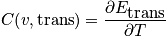
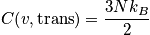
Rotational component of heat capacity
The relation below of the rotational component of heat capacity is used unless the temperature is very low or for
.
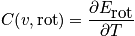
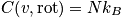
Vibrational component of heat capacity
The expression of the vibrational component of heat is below and is evaluated in two cases.
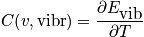
Case 1
The temperature can be evaluated in the case of temperature much lower than
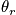
.
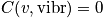
Case 2
An express of the vibrational component of heat capacity in the case of temperature greater than
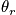
is below.
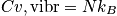
Total heat capacity
The total heat capacity is considered in two cases.
Case 1
Consider when the temperature is much less than
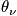
and greater than
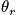
.
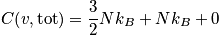
<P> </P>
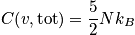
Case 2
An expression of the heat capacity is below in the case of the temperature greater than or equal to
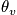
and much greater than
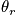
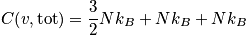
<P> </P>
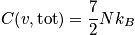
Comments
Define different kinds of motion. Solve the Schrodinger equation. Evaluate as well as possible. Take limits in the rotational case. Boltzman is a system approximation. Don't need to be too occupied with the math.
Configurational Properties
A figure below is of a mixture of atoms in a solid. Consider some arrangement on a lattice of atoms and vacancies or a binary mix. In general different arrangements are associated with different energies. Consider
sites with
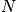
atoms of one kind. The term
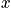
is the concentration.
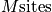
<P> </P>
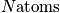
<P> </P>
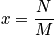
Assume now that the energy is only a function of concentration. Fix the concentration. With
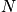
fixed, there is only one energy. Treat in terms of a canonical or microcanonical ensemble. The number of ways to distribut
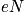
distinguishable particles on
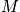
sites is expressed below in terms of
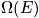
.
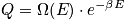
<P> </P>
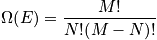
<P> </P>
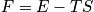
<P> </P>
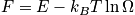
<P> </P>
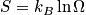
The term
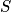
is the configurational entropy. Construct a phase diagram. Consider an electronic or vibrational shift. Configurational entropy is most important. Below is an expression simplified with Stirling's approximation. The configurational entropy can be expressed as a function of concentration.
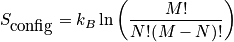
<P> </P>
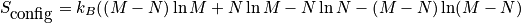
<P> </P>
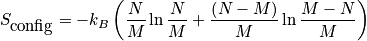
<P> </P>
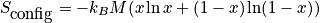
The expression above is of the ideal solid solution configurational entropy.
Calculate the propert of the system with increased
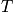
. Consider phase diagrams. An expression of Hemholtz free energy is below.
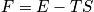
<P> </P>
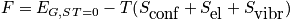
The largest impact is from the configurational entropy.