Be Careful
Some problems still need clarification. I will update them once we ask professor Cory.
Dynamics
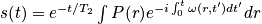
ω(r,t') = resonant frequency
P(r) = probability distribution
- Coherent - when ω is not a function of r (There are no interesting dynamics)
- Stationary - when ω is not a function of time (the system can be refocused by a π pulse for any time)
- Incoherent - stationary and not coherent, explicitly ω is a function of r (interesting question is the distribution of ω(r)
- Decoherent - when ω is a function of time and r, and the t dependence is stochastic/Marchovian (interesting dynamics: distribution of ω(r), spectral density of ω(r)
- Periodic - ω is a simple function of time (interesting dynamics: distribution of ω(r) at the characteristic frequency)
Periodic
Frequency that an arbitrary location will see
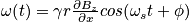
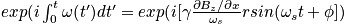

for one location in the sample
Static Spectrum
Problem 1
- Show that for average over φ, we get pure absorptive line-shape, and for a particular isochromat, average over φ in general has dispersive line-shape (Show the response in cylindrical coordinate)
- Normal shim: x,y (first order spherical harmonic). If there are terms x^2-y^2, xy, then the sideband will show up at twice Ω
- Calculate the FID and the spectrum for rotary vs non-rotary, then plot them on top of each other
Nuclear Spin
- Zeeman interaction
- Chemical shift : ppm variation due to chemistry -> transform as a tensor (orientation of the molecule matter)
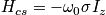
PAS (Principle axis system) = coordinate system that leave the molecule in diagonal ??
ω in transverse plane (slow) can be suppressed if rotation around z-axis is fast
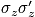
= secular part of the chemical shift, lead to small rotation in x-y direction
Problem 2
- Show that chemical shift tensor
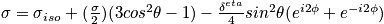



- Show that under random rapid motion spins
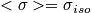
It average out any non-isometric parts, so we have a homogeneous sample. So the result does not depend on the orientation of the sample.
When η = 0 -> < 3cos(θ)^2 -1 > = 0, average over sphere
- η = 0 ; calculate the line-shape for static powder (constant orientation with magnetic field), η ≠ 0 ; reduce to a summation over η. [Hint: can be written in elliptical integral, check out appendix I ]
- Find σ(θ,φ), powder distribution of the sample (when spinning at the magic angle ?)
Decoherence
Bloc = field that a test spin would see (every spin averagely see the same distribution of B)
average vector still pointing along y => |Bloc> of time or ensemble = 0
Problem 3
- What is the contribution of the chemical shift anisotropy to T2?
Carl-Purcell Sequence
Problem 4
- Look at diffusive attenuation of water rotating in magnetic field gradient. (The faster you rotate it, the effective T2 is approaching T2)
Chemical Exchange
let
Problem 5
- Show the plot of the chemical exchange (when τ|ΔωA-ΔωB| approaching 1, the 2 peaks merge at the center) [Hint: check out appendix F]
Slow Exchange
choose Δ ≥ τ exchange, Δ << T1, Δ > T2
Problem 6
- Show that by collect this terms in slow exchange

then do phase cycle and collect data set
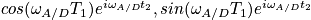
Then we get pure absorptive line-shape