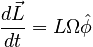A graphical approach to understanding the form of the centripetal acceleration.
Assumptions
We assume that we have uniform circular motion (motion with a constant radius and a constant speed centered at a fixed point in space).
The Diagram
The picture below illustrates the motion, with coordinates chosen so that the angular position at t = 0 is θ = 0.
To the right of the motion diagram is a vector diagram that shows the change in the velocity vector. The picture motivates the conclusion that if we take a very small Δt, the change in the velocity approaches:
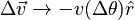
In the infinitesimal limit, this equation becomes:
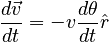
Using the fact that for uniform circular motion,
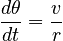
we arrive at the form of the centripetal acceleration:
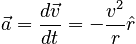
Analogy with Gyroscopic Precession
Consider a gyroscope precessing. The angular momentum will trace out a circle as shown below.
The similarity to the Δv diagram implies that we can write:
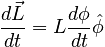
where the derivative of φ with respect to time is the angular frequency of precession, usually written as Ω:
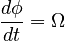
Fundamental Relationship for Gyroscopes
With that substitution, we have arrived at the fundamental relation for gyroscopes: