Page History

Tank Experiment

The second experiment was, in contrast, performed in the faster rotation speed of 10 rpm in order to replicate the regime in 30N – 60N and 30S – 60S. 

Similarly, to the first tank experiment, the particle tracker and thermometers were used to monitor the circulation and temperature in the tank. 

For the temperature profiles of each sensor, we found a periodic trend of temperature, which corresponds to the observed circulation pattern: circulating from the inner part to the outer part and vice versa

To verify the assumption that Eddy circulation plays role in transferring heat, we expect the calculated heat flux from the melt ice to be in the same magnitude as the heat flux from Eddy circulation.

We filled out parameters to the following equation.

z = 0.15 m

T’ = 1 K

ρ = 1000 kg/ m^3

Cp = 4.2 kJ/kgK

L = 333 kJ/kg

Initial Ice: 1.1 kg 

Note: To find T’, we first fit the temperature data with a loglog fit. This was chosen instead of a simple linear fit because when the hadley temperature data is plotted in loglog coordinates the line appears linear (see below), and the eddy data seems to follow a similar downward curve.

The eddy temperature data is plotted in loglog coordinates with the corresponding fit below (left). This fit was used as the mean temperature value, T. We then subtracted this value from the raw data, which gave the figure on the right. The loglog fit seems to be a good one, because once the mean downward trend is subtracted out, the residuals remain near zero and do not exhibit further upwards or downwards trends.

The root mean square was then taken, such that the full calculation process can be described by:

This gave a result of ~1ºC.

To find v', we find the mean of each sample track, subtract the velocity of each point with the mean, square each term, average them all, and take a square root of that average, which can be described by:

.
 

This gave a result of v’ = 0.94 cm/s = 0.0094 m/s

For the left hand side, we know the latent heat fusion coefficient of the ice, mass of the initial ice, and the time the ice took to be completely melt. For the right hand side, we assume the density of the liquid to be approximately equal to that of the water. So, we know the density, specific heat of the liquid, and v’ and T’ from thermometers and particle trackers. We also need to multiply a correction factor of 0.1 to the right hand side. After plugging all the values to the heat flux equation, we found find that the left hand side to be around 150 W and right hand side to be around 89 W.    

From the comparison of ice heat flux and calculated Eddy heat transport, we found that they were in almost the same magnitude—suggesting the relationship among them. 

Atmospheric Data

While atmospheric mean data could be used to study the Hadley circulation, eddies are shorter timescale phenomena and are calculated through deviations from the mean.

We were given data of v’t’ - the heat flux from the mean deviations for all latitudes, longitudes, and heights up to 100 mbar in the atmosphere. Looking at the vertical average of the deviations in January, we see particularly strong northward flux in regions 40ºN, over the Pacific and Atlantic Oceans. As the mean data revealed, the Hadley cell descends near 30º, with little There are also similar, though not nearly as strong, negative deviations around 40ºS as well. The values here are negative because they imply transport to the South Pole from the equator, and are not quite as large as those in the Northern Hemisphere due at least in part to the fact that the temperature gradient is larger in the northern hemisphere January, when it is winter there.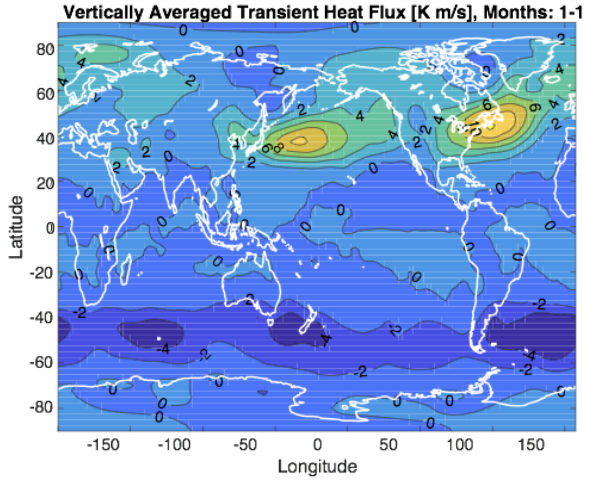

We can also plot the zonal average with height. The maximums at around 40ºN and S are evident here as well. An interesting feature is that for both latitudes, there exists a maximum near the surface, and one higher up in the atmosphere. The lower maximum, centered around 800 mbar, is a result of the large temperature gradient between the poles and equator near the surface. At higher altitudes, the temperature gradient lessens, but the meridional winds increase. The heat flux maximums near 200 mbars are a result of these stronger winds.

Finally, averaging both vertically and zonally gives the total northward flux at each latitude. Again, peaks occur just past 40 N and S. The peak in the Southern Hemisphere is very regular, while that in the northern hemisphere drops off less quickly at high latitudes. This lack of symmetry is likely a result of the fact that the majority of the continental land mass is located in the northern hemisphere, and the uneven surface leads to further atmospheric instabilities and eddies.

It is also useful to change the units of heat flux to Watts in order to compare our findings to the total energy flux of the earth. To do so, we vertically integrate our v’T’ zonal average and insert it into the following equation for energy flux: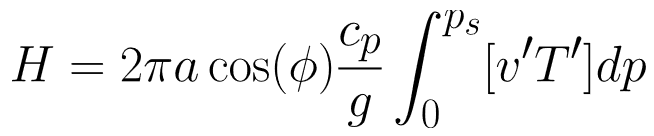

where a is the radius of the earth, ɸ is the latitude, Cp is the specific heat of air, g is gravitational acceleration. For a latitude of 40ºN, the equation gives a maximum energy flux of 1.1 PW (10^15 Watts).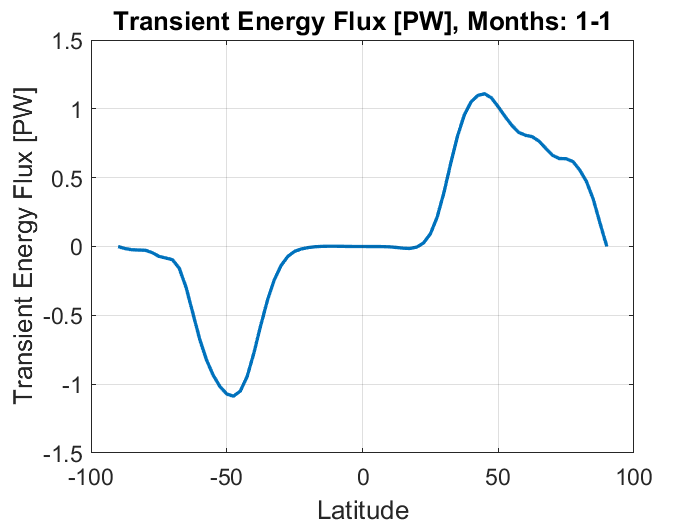

Comparing this figure to the graph of total energy flux in the atmosphere (the first figure in this section), we can see that it is on the same order of magnitude as the total transport of 5.5 PW at 40ºN; from our numbers, eddy transport would constitute 20% of the total at this latitude. This number seems slightly low however, considering that eddies are the predominant transport mechanism in mid-high latitudes. Our data has been filtered somewhat, to only account for the eddies that exist on timescales on the order of a week, but some eddies last only a couple days. There are also stationary eddies that remain relatively constant over several months. These are especially prominent in the Northern Hemisphere during the wintertime.

The figure below shows the total northward flux of sensible heat (not including latent heat), with breakdowns for transient eddies, stationary eddies, and mean meridional circulation. The units here are in K m/s the original units of our calculations, and winter (thin), summer (dashed) and yearly averages (thick) are plotted for each. The review here found a maximum transport for transient eddies of about 8 K m/s, twice as much as our calculations. Stationary eddies account for another 12 K m/s in the winter in the northern hemisphere, but disappear in the summertime. The mean meridional circulation, or Hadley circulation, is also plotted, and provides a maximum of over 30 K m/s near 10ºN and S. This circulation has a much smaller effect at high latitudes however, as our mean data also showed. One other significant source of energy transport is through latent heat, a topic not discussed in this project, but important to mention. Water that evaporates near the equator and is lifted and transported poleward condenses, releasing latent heat and further warming the higher latitudes.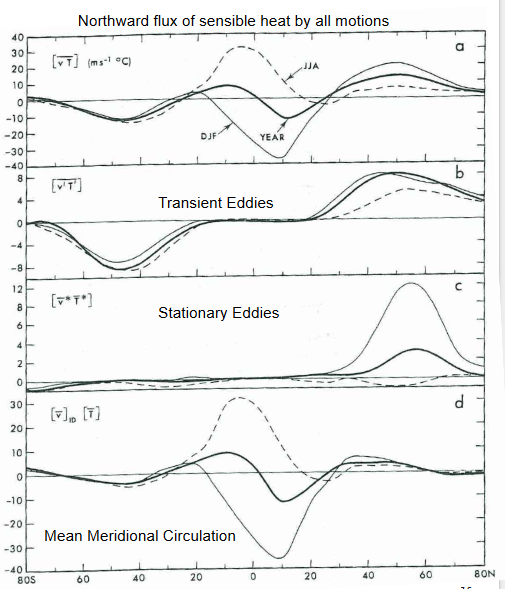

(Peixoto & Oort, 1992)